多値論理回路を用いた画像の輪郭抽出
1.はじめに
2値論理システムが"0","1"の2レベルの信号しかないのに対して,多値論理システムは信号を多レベル化することにより一千あたりの情報量を増大せ,近年,LSI・VLSIなどで問題となっている入力ピン数,内部配線面積を減少することができる.本研究では,データが多く処理が複雑になりがちな画像処理,特に輪郭抽出処理に多値論理を導入し,多値論理回路で設計することにより配線面積の削減,処理の効率化を目指している.
2.フィルタ5領域出力方式輪郭抽出処理
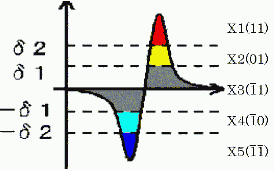
一般的な輪郭抽出フィルタであるフィルタ2値出力方式のラプラシアンフィルタではしきい値の設定を誤ると必要な情報が捨てられてしまう可能性がある.そこで,図1のようにフィルタ出力を5値にする方式を用いて,ファジイな情報を残すことにより,さらに必要な輪郭を抽出することができる.

2.1 フィルタ処理
しきい値で分割したLaplacian - Gaussianフィルタの出力値をX1からX5(としそれぞれ3値2桁であらわす.)
2.2 連結・補完処理
X1(X5)に隣接しているX2(X4)を連結する.また,X3から輪郭をして可能性のある画素を検出し補完を行う.
2.3 輪郭決定処理
連結・補完処理で得られた情報から輪郭を決定する.


(a)原画像
(b)フィルタ処理


(c)連結・補完処理
(d)輪郭決定
図2 (a)の原画像の用いた処理例
3. 8入力3値MAX,MIN回路
2.でフィルタ処理後の情報に3値2桁で符号化することにより,処理全体を通して主な演算処理を8入力3値MAX,MIN演算回路だけ構成することができる.8入力3値MAX,MIN演算回路をコンパクトかつ消費電力削減を考慮し設計することで本手法による輪郭抽出処理を回路化した際の回路面積,及び消費電力の削減を図る.
一方,ニューロンMOSFET(νMOSFET)は,2層ポリシリコンCMOSプロセスで作成され,特別な製造プロセスが不必要である.このため,2値論理回路に用いると回路のトランジスタ数の配線数が大幅に削減できることが報告されている.このνMOSFETを用いれば,フローティングゲート部において,電荷の加重平均がとれる.
上記のような理由から,8入力3値MAX,MIN演算回路をνMOSFETを用いた電圧モード多値論理回路で設計している.
3.1 νMOSFET
νMOSFETは,通常のMOSFETのゲートをフローティングゲートとして,複数の入力ゲートを容量結合しているから,複数の入力が可能となる.次式の入力電圧の加重平均φFにより,νMOSFETの動作が制御される.
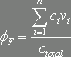
3.2 8入力3値MAX,MIN回路図
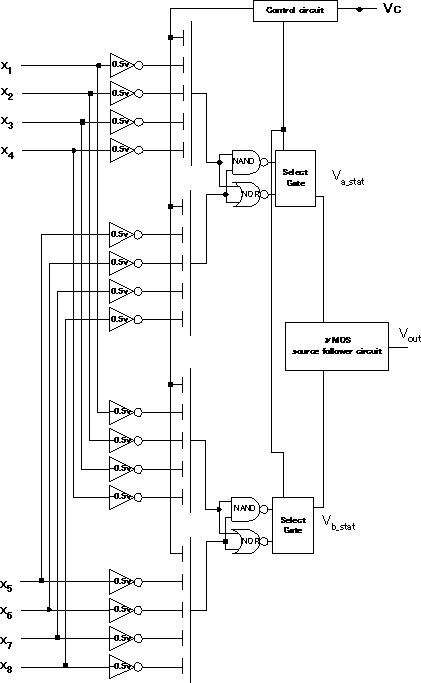
図3 8入力3値MAX,MIN回路図(MAX,MIN共有)
MAX回路かMIN回路かによって決まるしきい値をフローティングゲートに制御用の信号をバイアスすることにより設定し,フローティングゲートを共有したNAND回路とNOR回路の出力をセレクトゲートで選択することよってMAX回路とMIN回路を1つの回路にしている.図3に8入力3値MAX,MIN回路を示す.