制約充足問題の基本概念と事例
Basic Concepts and Examples

制約(Constraint)とは何か?


求める解が満たすべき命題．

制約充足問題 (CSP: Constraint Satisfaction Problem)


観察された現象や知識を制約の集まりとして表現し， それを満足する解の候補を求めること．

次のように定式化される．

1. n個の変数の集合 V: {v₁, v₂, ...,v_n}
2. 各変数 v_i ∈ D_i: 可能な値の集合(領域)
3. これらの変数の値が満足すべき制約条件を P: {P_i(...v_i...)}とする．ただし，v_i∈V．

制約充足問題への解集合は，与えられた全ての制約条件を満足する全て の n組の集合 (与えられた変数の張る空間の部分集合)．

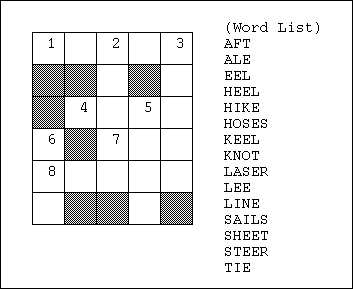
制約充足問題の例1: クロスワードパズル



• v_i: 縦/横の列 i
• D_i: i に入る可能性のある単語の集合
• 制約条件: 各 v_iに関する制約．交点において文字が一致する こと．

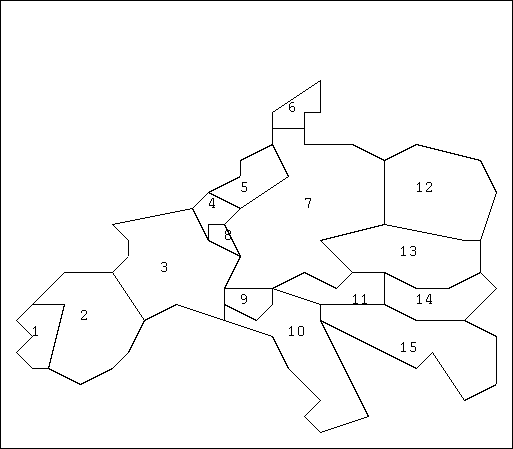
制約充足問題の例2: 地図の塗り分け問題



• v_i: 領域 i の色
• D_i: 4色．例えば {R,G,B,Y}
• 制約条件: 隣接する領域の色が異なること．

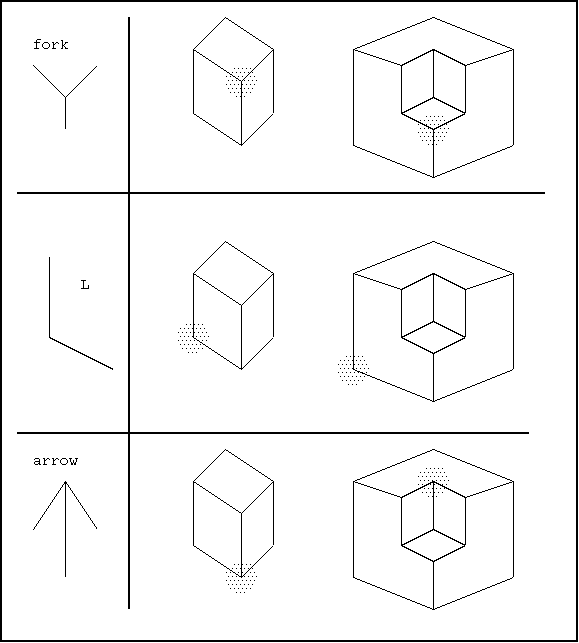
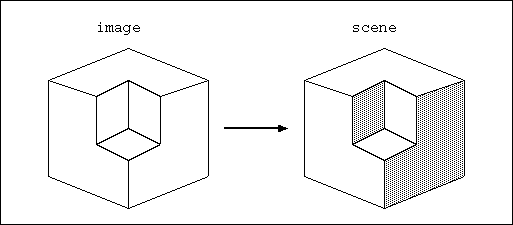
制約充足問題の例3: 線画解釈

輪郭抽出



2次元イメージから3次元シーンを復元する．次のような用語を用いる．

	シーン	イメージ
定義	3次元	2次元平面に投影された3次元
概念の例	頂点，エッジ，表面	ジャンクション，線分，領域

シーンとイメージの対応は以下の規則に従う．



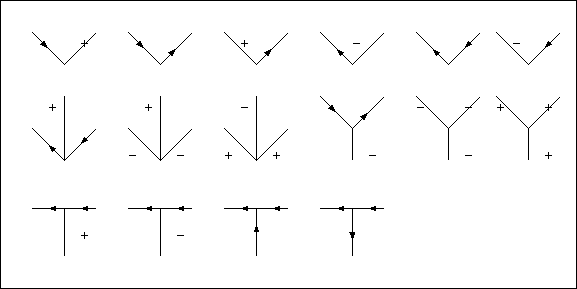
各エッジには，+, -, ← の3種類のラベルをつける．

• +は，凸のエッジで両側の平面がともに視点からみえるエッジを表す．
• -は，凹のエッジで両側の平面がともに視点からみえるエッジを表す．
• ←は，視点から見たとき両側の平面がエッジの片側に来ることを示す． その場合，一方の平面はもう一方の平面に遮られて見えない．矢印の向きは， 平面の対が矢印の方向に向かって右側に来るようにつける．

基本的なパターンへの可能なラベル付けは以下となる．



• L に対して6通り
• arrow に対して3通り
• forkに対して3通り
• Tに対して4通り

線画の各エッジへの衝突のないラベル付けを無矛 盾な解釈という．

...Return

• 講義の詳細