研究内容｜公立はこだてみらい大学｜複雑知能学科義永グループ

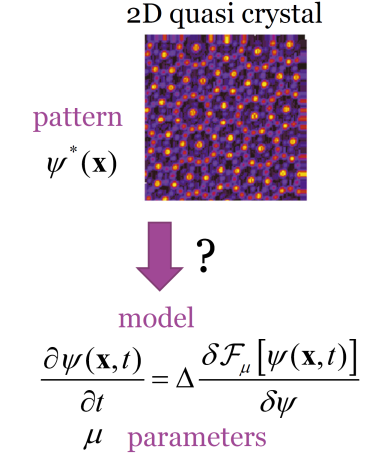
研究内容 Research

研究内容

ソフトマテリアルの物理学を中心に理論的な研究を行っています。ソフトマテリアルは、高分子、液晶、コロイドなどが含まれ、生体分子などもソフトマテリアルとみなすことができます。非平衡状態におけるソフトマテリアル、特に、エネルギーを消費しながら運動するものはアクティブソフトマテルなどと呼ばれています。細胞運動や生命現象で現れるパターンはソフトマテリアルの集団として数理的に理解できることもあって、これらに注目して研究を行っています。最近は、機械学習によって、ソフトマテリアルの支配方程式を推定する方法や、材料科学へ応用についての研究にも取り組んでいます。

機械学習とソフトマターの物理

ソフトマテリアルの支配方程式は、これまで、過去の研究や物理法則を基に導出されてきました。しかし、ソフトマテリアルは非常に複雑で、大自由度からなり、階層性を持っているために、支配方程式を得るためには膨大な時間をかけた試行錯誤を行うしかありませんでした。最近の機械学習の発展により、支配方程式をデータや目的となる情報から推定することへの期待が高まってきています。比較的単純な方程式を推定することは可能になってきていますが、ソフトマテリアルのような複雑な問題には、現在の手法では不十分です。そこで我々は、ソフトマテリアルの構造形成の支配方程式を推定する手法の開発に取り組んでいます。

ミクロ相分離パターンから支配方程式を推定する

目的の構造やパターンが手元にある時、その構造がどのような方程式で作ることができるのかは重要な問題です。実験的に得られた構造を再現できる方程式が分かれば、その構造形成のメカニズムを理解するための大きなヒントになります。我々は、たった1つの構造データから偏微分方程式を推定する手法について研究を行っています。

目的の自己凝集構造を実現するためのコロイド粒子のデザイン

最近の実験技術の発展により、様々な、ナノメートル、マイクロメートルのコロイド粒子の形状や表面構造、相互作用ポテンシャルを実現することが可能になっています。その結果、ダイヤモンド格子などの複雑な構造を、原子ではなくコロイド粒子を用いて、自己凝集（self-assembly）によって作成することが可能になっています。一方、「欲しい」構造があった時に、どのように粒子をデザインすればよいのかというのは、まだまだ困難な問題です。私たちは、パッチ粒子を用いて、目的の構造を実現するためのパッチのデザインの研究を行っています。

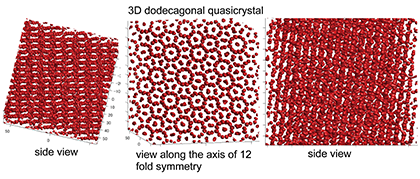
準結晶構造

準結晶は、結晶のような秩序構造を持ちながら、結晶のように周期性を持たない構造です。自然界には様々な対称性を持つ準結晶が存在することが知られていますが、その形成メカニズムはまだ未解明です。私たちは、phase-field crystalモデルと呼ばれる連続場の方程式を用いて、二次元や三次元の準結晶の形成過程について研究を行っています（右図は二次元と三次元の準結晶の例)。

他のマテリアルズサイエンスへの広がり

数理的には、ソフトマテリアルの研究で用いられている理論は他の材料科学に応用することができます。パターンを記述する方程式であるphase-field crystalモデルは、材料科学でよく用いられるphase-fieldモデルの拡張として、結晶の欠陥のダイナミックスを記述するために用いられています。また、磁性体に見られるスピン波は、液晶で用いられるモデルと多くの類似性を持っています。私たちは、材料科学という広い分野に共通する原理を明らかにし、支配方程式を推定できるように研究に取り組んでいます。

機械学習と方程式推定について講演はこちらから視聴できます。

- ベイズ推定を用いた画像パターンからの支配方程式の選択 (2020)
資料はこちらです。
- 材料科学へのデータ科学的なアプローチ

- Newton Institute seminar (2023)
New statistical physics in living matter: non equilibrium states under adaptive control

- 九州大学 IMI共同利用統計数学×情報×物質セミナー (2023)
自己組織化による構造形成のための数理モデルの推定

アクティブマターの数理 -- 自発運動する粒子や液滴

生命現象において生物はエネルギーを消費しながらその機能を実現しています。中でも細胞運動は、細胞が外力によって押されることなく動く現象です。これはATPの加水分解によるエネルギーを消費して生成するアクティブなストレスによって実現しています。アクティブマターと呼ばれる研究は、このような自発的な運動や変形を理解することです。最近の実験で、化学反応を使ってまるで生きているように物体が動く現象が見い出されています。私たちは、数理モデルを用いて、粒子や液滴の自発的運動や変形のメカニズムについて研究を行っています。

アクティブ液晶の液滴：細胞運動のモデル

細胞運動は非常に複雑な現象ですが、運動メカニズムは、アクティブストレス、Treadmilling、ブレッビングなどが知られています。ここでは、液滴の中にアクティブ液晶が封入されている系を考察し、アクティブストレスによっていかに運動が生じるのかを調べました。アクティブストレスが強く、またcontractileである場合には、直線運動が回転運動に分岐し、さらに乱れた運動を引き起こすことを明らかにしました。

温度勾配による粒子の運動とヤヌス粒子の自己泳動

温度泳動は温度勾配によって物体が動く現象です。これは電場による物体の運動（電気泳動）や濃度勾配による運動（拡散泳動、あるいは浸透泳動)現象と同様のものである。温度泳動は150年以上前から知られているが、その微視的なメカニズムはいまだ多くのことが分かっていません。私たちは、流体モデルによって温度勾配によって駆動される粒子の運動について研究を行っています。さらに、最近ヤヌス粒子を用いて、一様な環境でも、粒子が自発的に周囲に勾配を形成して運動することが実験的、理論的に明らかになっています。これらの問題を理論的に研究しています。

マランゴニ効果による液滴の運動と変形

自発運動による一方向の運動は、物体の内在的な非対称性だけでなく、自発的に回転対称性を破ることによって実現することができます。後者は、平衡状態における相転移のように、系の非線形性と関連していて、ある種の非平衡相転移というものです。また、非線形ダイナミックスの分野ではドリフト分岐やドリフト不安定性と呼ばれています。我々は流体モデルを用いてマランゴニ効果による非平衡相転移について研究を行っています。

アクティブマターに関するの講演はこちらから視聴できます。

- Newton Institute(mp4 movie) at the workshop "Dynamics of Suspensions, Gels, Cells and Tissues"
- Newton Instituteseminar (mp4 movie)
- Kavli Institute for Theoretical Physics

細胞生物における数理

たんぱく質の波の形成

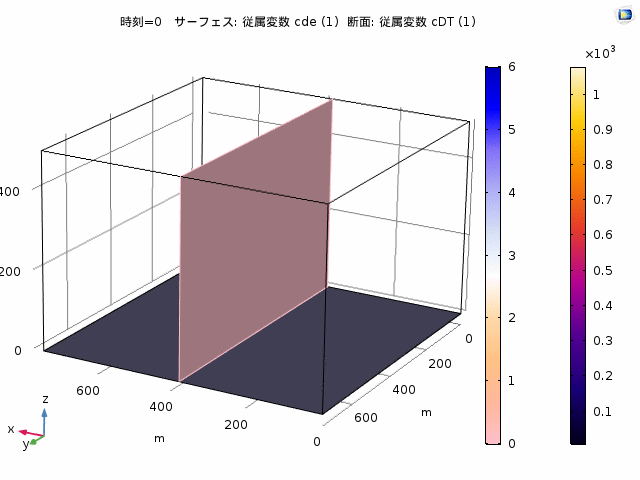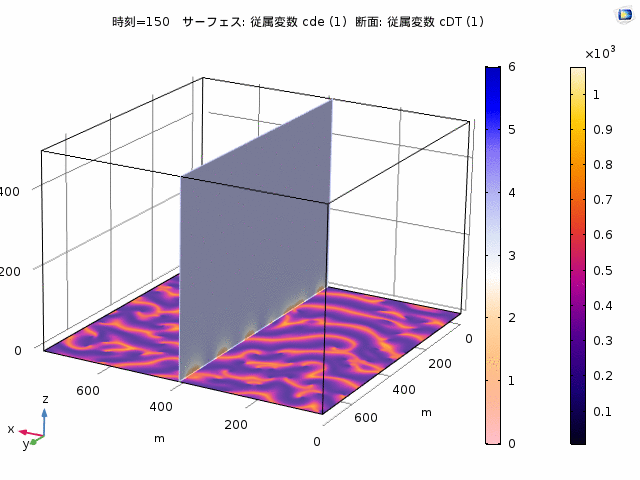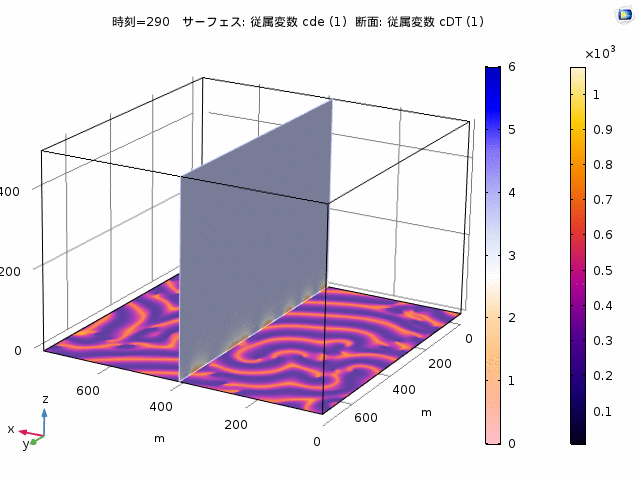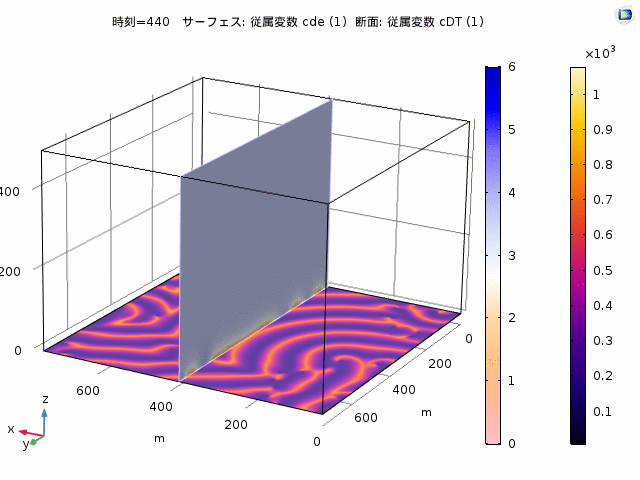
大腸菌の細胞分裂において、Minたんぱく質が分裂中心を決める重要な役割を果たしています。最近、人工細胞において、平面膜や球面状膜でMinたんぱく質の波が再構成できるようになってきています。Minたんぱく質は、膜面とバルクの間を行き来しながら拡散し、他のたんぱく質と相互作用することで波を形成します。この現象は反応拡散方程式によってモデル化でき、2次元空間である膜面と3次元のバルクを両方取り扱わないといけません。私たちは、平面膜と、実際の細胞に近い球状のドメインで、境界とバルクが結合した反応拡散方程式の解析を行っています。

細胞骨格におけるアクチンの極性分布形成

ストレスファイバーは、細胞の力学特性を担っています。主要な要素は、アクチンフィラメント、ミオシンなどの分子モーター、そして架橋たんぱく質であり、他にも様々なタンパク質が機能に関わっていると言われています。この研究の目的はストレスファイバーを非平衡状態におけるソフトマターとして理解することです。

非平衡状態における高分子

ソフトマターの動力学は生命現象や身の回りに見られる様々な材料を理解するために重要な役割を果たしています。例えばシェービングジェルを手に乗せてこすると泡になることは経験的には知られていますが、実はこの現象は、非線形非平衡なで、モデル化し解析することは非常に困難です。私たちは、高分子の動力学について様々な研究を行っています。