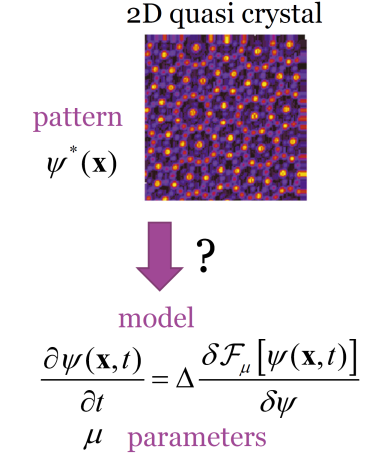
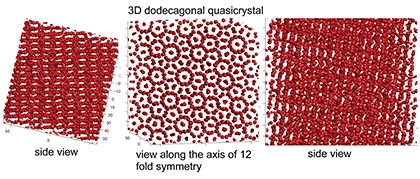
Quasicrystals in Soft Materials

Quasicrystals have rotational order, but do not have translational order. Many quasicrystals have been found in metallic alloys, but recently they are also found in soft materials, such as block copolymers, sufactantsm and colloids. We are developing a simple model to reproduce various quasicrystals in two and three dimensions (right figures).

Inverse structural design of colloidal particle assemblies

Quasicrystals have rotational order, but do not have translational order. Many quasicrystals have been found in metallic alloys, but recently they are also found in soft materials, such as block copolymers, sufactantsm and colloids. We are developing a simple model to reproduce various quasicrystals in two and three dimensions.

Application to other materials

Our theoretical approaches are not limited to soft materials, but may be applied to other materials. The phase-field crystal model may be applied to kinetics of dislocations and disclinatinos in crystalline materials. We are also working on spin waves, which can be described by nonlinear partial differential equations.

Self-propelled particles and drops

Biological systems consume energy and exhibit their functions. Among the variety of phenomena, we are particularly interested in cell motility. Interestingly, cells can move without any external force. This is achieved by active force (stress) generation using energy of ATP. The goal of this study is to understand the mechanism of self-propulsion. As a first step, we are now investigating model chemical systems in which particles and drops move spontaneously.

Thermophoresis

Thermophoresis is a phenomenon of directional motion under temperature gradient. This is similar to electrophoresis under an electric field and osmophoresis (difussiophoresis) under a concentration gradient. It was found back in 1856, though the mechanism, particularly microscopic and mesoscopic aspects, remains unclear despite of intensive studies. We have developed hydrodynamic equations, and investigated flow induced by temperature gradient. This phenomenon is strongly dependent on surface properties of objects in phoretic motion.

Deformation induced spontaneous motion

An important observation for motile cells is that they can deform. Recently, it has been suggested that there is strong correlation between deformation and motion. Although cells are very complex, we believe the essence is shared with artificial model systems which are simpler and exhibit spontaneous motion and deformation. With the aid of hydrodynamics, we are trying to clarify the relation between deformation and motion.

Drift instability of a drop driven by Marangoni flow

The directional motion of self-propulsion arises either from intrinsic asymmetry of the systems or spontaneous break of rotational symmetry. The latter is related with nonlinear nature of the systems as phase transitions in equilibrium systems. We are now interested in the nonequilibrium phase transition between stationary and moving stales. This has been studied in the field of nonlinear dynamics as drift instability. We have developed hydrodynamics describing this instability for the Marangoni effect.

My recent talk is here.
- Newton Institute(mp4 movie) at the workshop "Dynamics of Suspensions, Gels, Cells and Tissues"
- Newton Instituteseminar (mp4 movie)
- Kavli Institute for Theoretical Physics

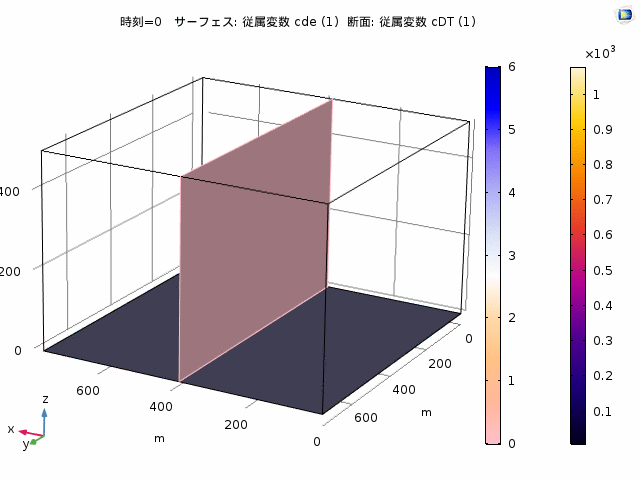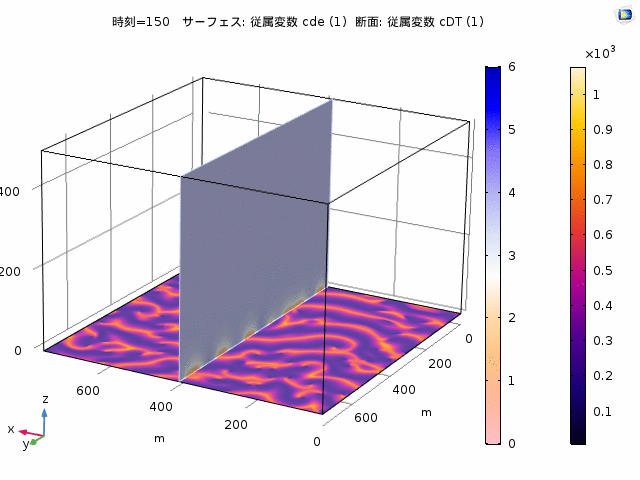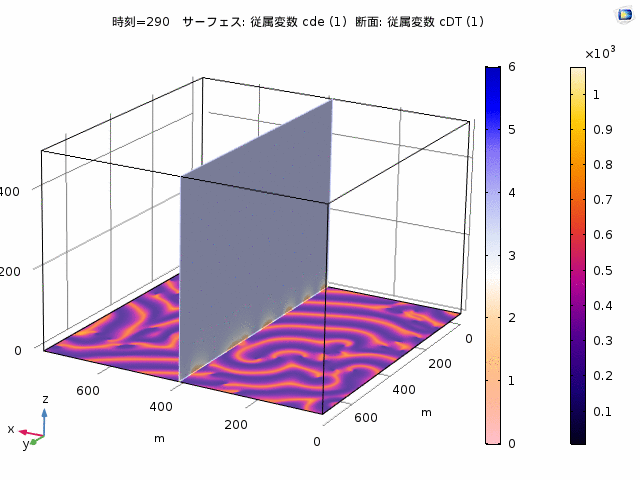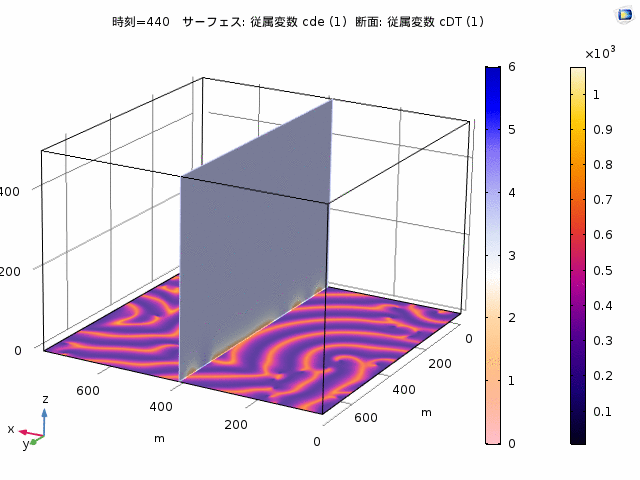
Pattern formation of Min proteins

Min portens are known to be essential ingredients to determine the cell centre during cell division of E-coli. Nonlinear waves of MinD and MinE occur by their nonlinear interactions. In cells, standings waves, also called pole-to-pole oscillation, are relevant because their node sets the cell centre precisely. Interestingly, artificial systems that have Min proteins together with other ingredients may show waves (see the right figure). The system has surface of a membrane and bulk of cytosol. Min proteins exhbit both chemical reactions and diffusion on the surface and in the bulk. We propose and analyse a model expressed by nonlinear reaction-diffusion equations, and found that the nonlinear waves occur both flat (top figure) and spherical (bottom) geometries. Moreover, for the spherical geometry, which is closer to the shape of a cell, the effect of confinement plays a significant role for the wave generation.

Polarity pattern of stress fibre

Stress fibres are key elements of mechanical aspects of cells. Main ingredients are actin filaments, myosin II, and a-actinin. Many other proteins have also been found and considered to function. Our purpose in this study is to model stress fibres as assemble of filaments in nonequilibrium systems.
Actin filaments have polarity, that is, they have plus (barbed) and minus (pointed) ends. Several polarity patterns have been found in cells, for instance graded polarity, alternating polarity, and uniform one. The alternating polarity looks similar to muscle. However, the relation between polarity and mechanical properties are still unknown. We show active stress generated by molecular motors (myosin filaments) determines polarity patterns.